ベクトルの大きさ(norm)を計算するには、NumPyのnp.linalg.norm関数を使用するのが最も効率的です。本記事では、NumPyでベクトルのnormを計算する複数の方法とそのパフォーマンスを比較します。
ベクトルの大きさ(norm)の求め方
ベクトルの大きさ(norm)は、ベクトルの各要素の二乗和の平方根として計算されます。数学的には以下の式で表されます。
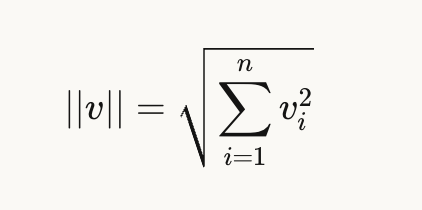
NumPyでは主に2つの方法でベクトルのnormを計算できます。
np.linalg.norm関数を使用する方法np.sqrt(np.sum(x**2))を使用する方法
np.linalg.norm
np.linalg.normはNumPyの線形代数モジュールに含まれる関数で、ベクトルやマトリクスのnormを計算するために最適化されています。
構文
np.linalg.norm関数は以下のような構文で使用します。各パラメータを適切に設定することで、様々な種類のnormを計算できます。
numpy.linalg.norm(x, ord=None, axis=None, keepdims=False)x: 入力配列。ベクトルまたは行列を指定します。ord: normの種類を指定するパラメータです。デフォルトはフロベニウスnormで、ベクトルの場合は2-norm(ユークリッドノルム)になります。1を指定すると1-norm(マンハッタン距離)、infを指定すると無限大ノルムになります。axis: 計算を行う軸を指定します。例えば2次元配列でaxis=1を指定すると行ごとのnormを計算します。keepdims: 結果の次元を入力と同じに保つかどうかを指定します。Trueにすると、計算された軸は長さ1の次元として保持されます。
コード例
以下のコードは1次元ベクトルのnormを計算する例です。
import numpy as np
# 1次元ベクトルの例
vector_1d = np.array([3, 4])
norm_1d = np.linalg.norm(vector_1d)
print(f"1次元ベクトル {vector_1d} のnorm: {norm_1d}")
# 出力: 1次元ベクトル [3 4] のnorm: 5.0
# 2次元ベクトルの例
vector_2d = np.array([[1, 2], [3, 4]])
norm_2d = np.linalg.norm(vector_2d)
print(f"2次元ベクトル全体のnorm: {norm_2d}")
# 出力: 2次元ベクトル全体のnorm: 5.477225575051661
# 行ごとのnormを計算
row_norms = np.linalg.norm(vector_2d, axis=1)
print(f"各行のnorm: {row_norms}")
# 出力: 各行のnorm: [2.23606798 5. ]
# 列ごとのnormを計算
col_norms = np.linalg.norm(vector_2d, axis=0)
print(f"各列のnorm: {col_norms}")
# 出力: 各列のnorm: [3.16227766 4.47213595]np.sqrt(np.sum(x**2))
NumPyの基本関数を組み合わせてベクトルのnormを計算することもできます。この方法は直感的で理解しやすいという利点があります。
構文
基本関数を組み合わせてnormを計算する方法は、以下のような構文で実装できます。この方法はnp.linalg.normよりも直感的に理解しやすい利点があります。
np.sqrt(np.sum(x**2, axis=None))x: 入力配列。ベクトルまたは行列を指定します。axis: 合計を計算する軸を指定します。例えばaxis=0で列方向、axis=1で行方向の合計を計算します。指定しない場合は配列全体の合計を計算します。
コード例
以下のコードは基本関数を使用してnormを計算する例です。
import numpy as np
# 1次元ベクトルの例
vector_1d = np.array([3, 4])
norm_1d = np.sqrt(np.sum(vector_1d**2))
print(f"1次元ベクトル {vector_1d} のnorm: {norm_1d}")
# 出力: 1次元ベクトル [3 4] のnorm: 5.0
# 2次元ベクトルの例
vector_2d = np.array([[1, 2], [3, 4]])
norm_2d = np.sqrt(np.sum(vector_2d**2))
print(f"2次元ベクトル全体のnorm: {norm_2d}")
# 出力: 2次元ベクトル全体のnorm: 5.477225575051661
# 行ごとのnormを計算
row_norms = np.sqrt(np.sum(vector_2d**2, axis=1))
print(f"各行のnorm: {row_norms}")
# 出力: 各行のnorm: [2.23606798 5. ]
# 列ごとのnormを計算
col_norms = np.sqrt(np.sum(vector_2d**2, axis=0))
print(f"各列のnorm: {col_norms}")
# 出力: 各列のnorm: [3.16227766 4.47213595]速さの比較
np.linalg.normとnp.sqrt(np.sum(x**2))のパフォーマンスを比較してみましょう。特に大きな配列では、最適化されたnp.linalg.normの方が高速である傾向があります。
import numpy as np
import time
# 大きな配列を生成
large_vector = np.random.rand(1000000)
# np.linalg.normの計測
start_time = time.perf_counter()
norm1 = np.linalg.norm(large_vector)
end_time = time.perf_counter()
linalg_time = end_time - start_time
# np.sqrt(np.sum(x**2))の計測
start_time = time.perf_counter()
norm2 = np.sqrt(np.sum(large_vector**2))
end_time = time.perf_counter()
basic_time = end_time - start_time
print(f"np.linalg.norm の実行時間: {linalg_time:.6f}秒")
# 出力例: np.linalg.norm の実行時間: 0.000336秒
print(f"np.sqrt(np.sum(x**2)) の実行時間: {basic_time:.6f}秒")
# 出力例: np.sqrt(np.sum(x**2)) の実行時間: 0.002417秒
print(f"np.linalg.norm は np.sqrt(np.sum(x**2)) の約 {basic_time / linalg_time:.2f} 倍速い")
# 出力例: np.linalg.norm は np.sqrt(np.sum(x**2)) の約 7.19 倍速い実行環境によって異なりますが、一般的にnp.linalg.normの方が高速です。これはnp.linalg.normが最適化されたBLAS(Basic Linear Algebra Subprograms)ライブラリを使用しているためです。
まとめ
NumPyでベクトルのnormを計算する場合はnp.linalg.norm関数を使用することをおすすめします。np.linalg.normは以下の点で優れています。
- 処理速度が速い(実験では約7倍の速度差)
- コードが簡潔で読みやすい
- 様々な種類のnormに対応している
大規模なデータや繰り返し計算が必要な場合は特にnp.linalg.normの利点が顕著になります。両方の方法で計算結果は同じですが、パフォーマンスを重視するならnp.linalg.normが最適な選択です。


