【dot】numpyでベクトルの内積を求める方法を解説

Python

UdemyのおすすめPython講座はこちら

本記事では、numpyでベクトルの内積を求める方法を解説します。numpy.dot関数を使うことで、ベクトル同士の内積計算や行列演算を簡単に実行できます。

ベクトルの内積

ベクトルの内積は、2つのベクトルの対応する要素を掛け合わせて、その結果を全て足し合わせた値です。numpy.dot関数を使用することで、効率的に内積を計算できます。

数学的定義

2つのベクトルの内積は以下のように定義されます。

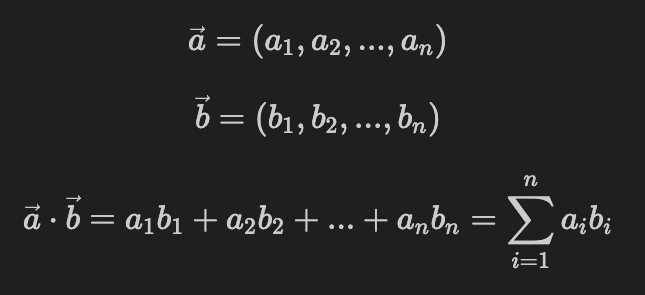
具体例

内積の計算例です。

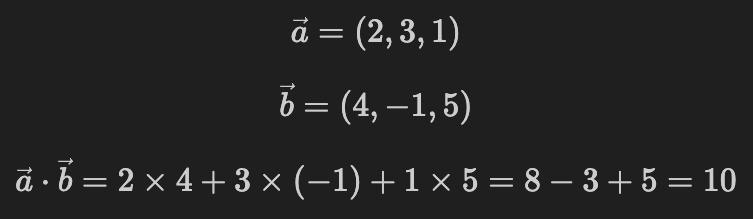
基本的な使い方

1次元ベクトルの内積

2つの1次元ベクトルの内積を計算する基本的な例です。

import numpy as np

# 例と同じベクトルを定義
a = np.array([2, 3, 1])
b = np.array([4, -1, 5])

# 内積を計算
result = np.dot(a, b)
print(result)
# 出力: 10

2次元配列での内積

2次元配列同士の内積（行列の積）を計算する例です。

import numpy as np

# 2つの行列を定義
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 行列の積を計算
result = np.dot(A, B)
print(result)
# 出力: [[19 22]
#       [43 50]]

ベクトルと行列の積

ベクトルと行列の積を計算する例です。

import numpy as np

# 行列とベクトルを定義
matrix = np.array([[1, 2, 3], [4, 5, 6]])
vector = np.array([7, 8, 9])

# 行列とベクトルの積を計算
result = np.dot(matrix, vector)
print(result)
# 出力: [ 50 122]

詳細な設定

出力先の指定

計算結果を既存の配列に格納したい場合、out引数を使用できます。

import numpy as np

# 2つのベクトルを定義
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 結果を格納する配列を準備
output = np.empty(1)

# 結果を指定した配列に格納
np.dot(a, b, out=output)
print(output)
# 出力: [32.]

注意点

行列の積はmatmulまたは@演算子を使用

numpy 1.10以降では、行列の積にはnp.matmulまたは@演算子の使用が推奨されています。np.dotは主にベクトルの内積計算に使用することが適切です。

matmul関数と@演算子を使用して行列の積を計算する例です。

import numpy as np

# 行列を定義
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# matmulを使用した行列の積
result_matmul = np.matmul(A, B)
print(result_matmul)
# 出力: [[19 22]
#       [43 50]]

# @演算子を使用した行列の積
result_at = A @ B
print(result_at)
# 出力: [[19 22]
#       [43 50]]

np.innerとの違い

np.dotとnp.innerは似た機能を持ちますが、多次元配列での動作が異なります。np.dotは一般的な行列積を計算し、np.innerは各行ベクトル同士の内積を計算します。

1次元ベクトルでは同じ結果になりますが、2次元配列では異なる結果を返します。

import numpy as np

# 1次元ベクトルの場合（同じ結果）
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# どちらも 1*4 + 2*5 + 3*6 = 4 + 10 + 18 = 32
dot_result = np.dot(a, b)
inner_result = np.inner(a, b)
print(f"np.dot: {dot_result}")
print(f"np.inner: {inner_result}")
# 出力: np.dot: 32
#       np.inner: 32

# 2次元配列の場合（異なる結果）
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# np.dot: 行列の積を計算
# A[0,:] @ B[:,0] = [1,2] @ [5,7] = 1*5 + 2*7 = 19
# A[0,:] @ B[:,1] = [1,2] @ [6,8] = 1*6 + 2*8 = 22
# A[1,:] @ B[:,0] = [3,4] @ [5,7] = 3*5 + 4*7 = 43
# A[1,:] @ B[:,1] = [3,4] @ [6,8] = 3*6 + 4*8 = 50
dot_result = np.dot(A, B)

# np.inner: 各行同士の内積を計算
# A[0,:] @ B[0,:] = [1,2] @ [5,6] = 1*5 + 2*6 = 17
# A[0,:] @ B[1,:] = [1,2] @ [7,8] = 1*7 + 2*8 = 23
# A[1,:] @ B[0,:] = [3,4] @ [5,6] = 3*5 + 4*6 = 39
# A[1,:] @ B[1,:] = [3,4] @ [7,8] = 3*7 + 4*8 = 53
inner_result = np.inner(A, B)

print(f"np.dot:\n{dot_result}")
print(f"np.inner:\n{inner_result}")
# 出力: np.dot:
#       [[19 22]
#        [43 50]]
#       np.inner:
#       [[17 23]
#        [39 53]]

配列の次元に注意

np.dotを使用する際は、配列の次元と形状に注意が必要です。内積を計算するためには、適切な次元の組み合わせが必要です。

次元が合わない配列同士で内積を計算しようとした場合のエラー例です。

import numpy as np

# 次元が合わない例（エラーになる）
try:
    a = np.array([1, 2, 3])
    b = np.array([4, 5])  # 長さが異なる
    result = np.dot(a, b)
except ValueError as e:
    print(f"エラー: {e}")
# 出力: エラー: shapes (3,) and (2,) not aligned: 3 (dim 0) != 2 (dim 0)

まとめ

numpy.dot関数は、ベクトルの内積計算において重要な機能を提供します。基本的な1次元ベクトルの内積から、2次元配列での行列演算まで幅広く対応できます。ただし、行列の積については、より明確な意図を示すnp.matmulや@演算子の使用を検討することが推奨されます。適切な次元の配列を使用し、必要に応じてout引数で出力先を指定することで、効率的な数値計算が可能になります。

タイトルとURLをコピーしました